Hello David,
Thanks for the interesting question !
BLUF answer : yes but 
Now for the wall of text : a non detect basically corresponds to the information : anywhere between 0 and the LOQ.
Traditional estimation methods for distributional parameters (e.g. estimating mean, variability, percentiles), cannot incorporate this type of information ([0-LOQ]) as they are designed to receive single values ; hence the need to replace [0-LOQ] with something like LOQ/2 or some other value. These replacements generally have catastrophic impact on parameter estimation, in particular in the estimation of uncertainty.
Bayesian analysis does not require to choose a replacement value because its use of observations is through what is called the likelihood, and the likelihood of of an observation defined as [0-LOQ] is as easy to determine as that of e.g. 0.1 ppm. So a big advantage of Bayesian analysis is that you don’t have to replace the actual result with any arbitrary value.
That said one must bear in mind that knowing that x=0.1ppm is very different from knowing that it is between 0 and LOQ in terms of information about the question of interest. This is especially true since we study lognormal data, which we log-transform prior to analysis : so we actually tell the statistical engine : the log transformed value is between -infinity and ln(LOQ).
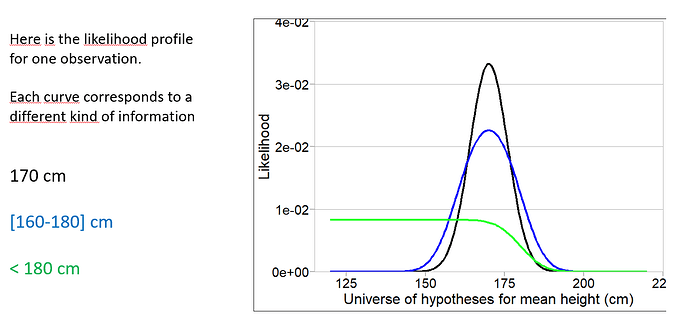
To illustrate a bit more quantitatively this difference in informativeness. The picture below shows 3 shapes of likelihood for the estimation of the mean of a normal distribution based on one observed value, one value known as a range, and one censored value. The black curve tells us that one observation at 170cm suggest the mean of the underlying distribution would be mostly between 155 and 185 cm. Knowing only that the observation was between 160 and 180 causes the likelihood to get wider : less information, the mean could now be anywhere between 145 and 195. Finally the green curve shows the likelihood associated with <180 cm. We can only infer from that that the mean is probably lower than 190 or so.
To come back to using expostats with a lot of non detects: the calculation will run but you will observe a very large residual uncertainty because of the lack of info embedded in NDs. This also means that indeed adding one single observed point can change things drastically, beauce one observed point contains a lot more info. Finally lack of information from the data means that the results rely more heavily on the prior assumptions in the calculation engine, so you could see very different results for the same data between tools not using the same set of priors.
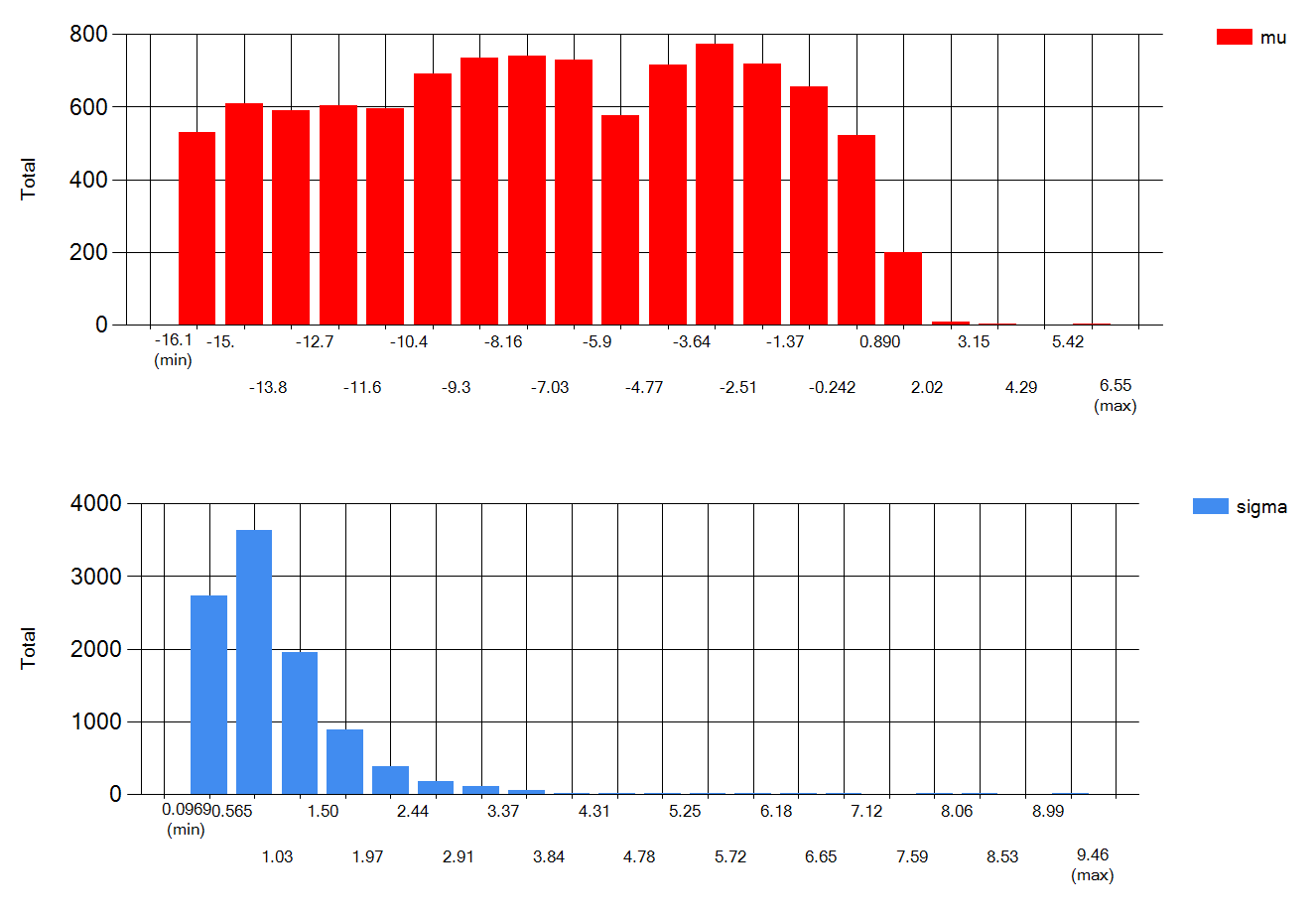
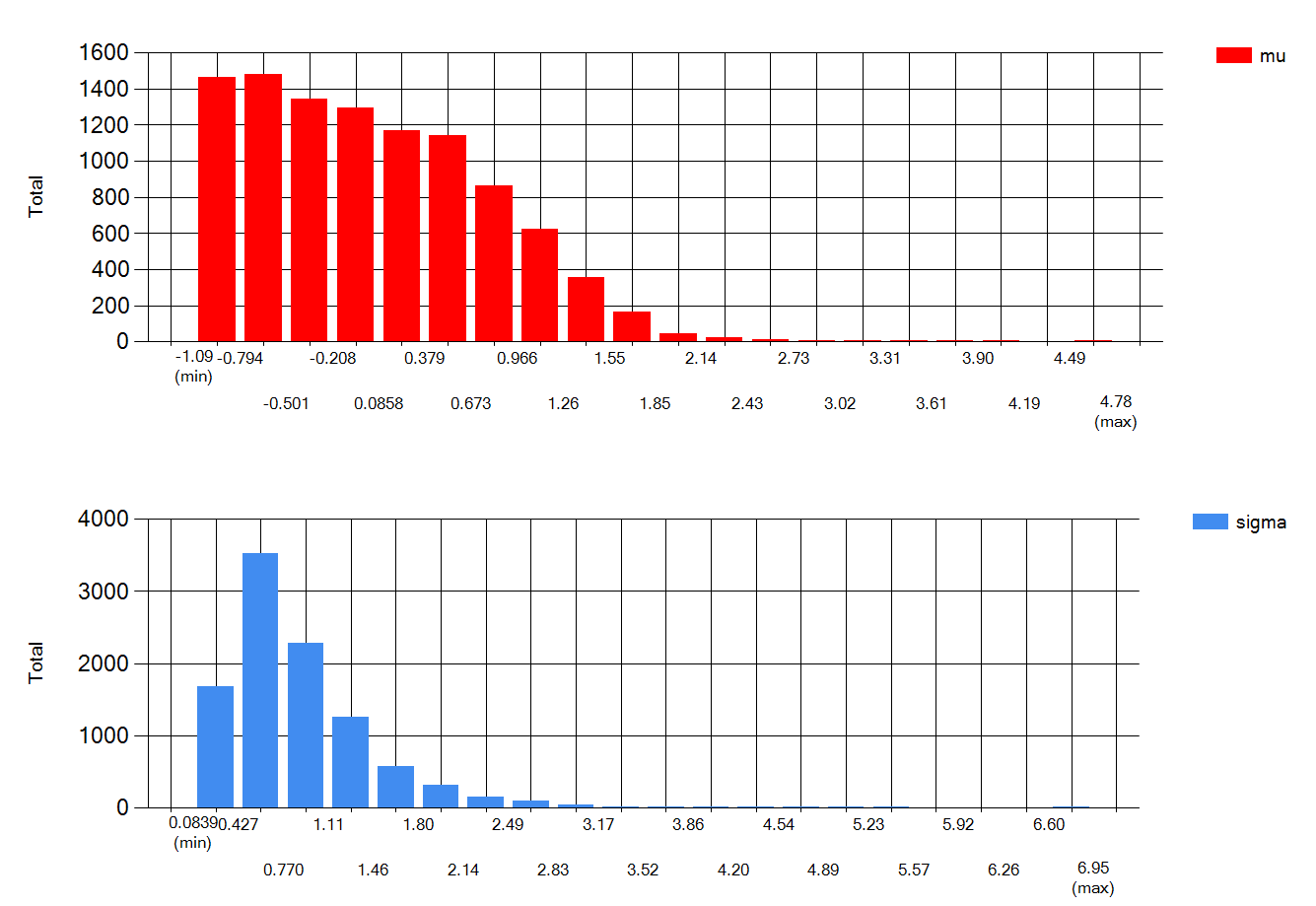
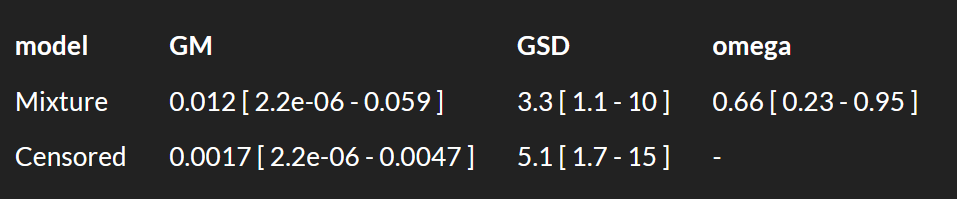
Specifically for IH data, I wouldn’t be to worried by lots of NDs when the LOQ is quite lower than the OEL. However I would be more careful with ND only data when LOQ is rather close to the OEL. As an example, look at what happens when you input <100 3 times in expostats with OEL=100. GM is reported to be anywhere between 10^-7 and 30, GSD anywhere between 1.3 and 10 : we know very little. The BDA chart though suggest there is at most 6% chance that the 95th percentile is above the OEL. However if I change the prior assumptions (e.g. assuming that the true GM cannot be lower than 1 ppm) , these chances increase to 25% (this cannot yet be done in the public expostats).
Trying to get to a bottomline : A high proportion of NDs is OK in Expostats but, especially when the LOQ is close to the OEL, the risk results will depend heavily on internal assumptions. Also RE the difference in likelihood between a range and < : use the range capability of expostats (unique to expostats) whenever you can force the lab to tell you “detected but not quantified” instead of just “not quantified”.
Jérôme