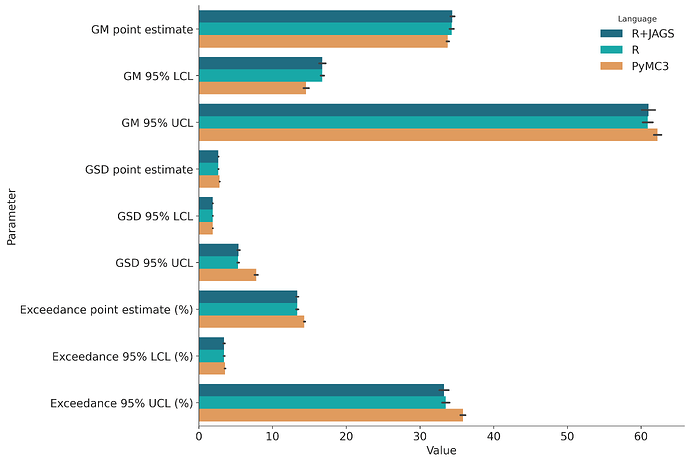Differences Between Bayesian Samplers - Informedvar model

Sampling strats and stats
1

I’m currently trying to replicate the WebExpo models in PyMC. Half learning / half stubborn with picking up R.

I have a ‘working’ model based on the informedvar, however when utilising the data from Section 4.3.3 of the WebExpo report for comparison against different programming languages, I am getting “slightly” different results. Typically, my GM point estimates are slightly lower, and my GSD point estimates are slightly higher.

From what I can suspect, it could be how censored data is handled between your implementation (I suspect) vs how PyMC handles censored data natively. The default censored class doesn’t impute the censored data based on uncensored values, it integrates the censored values out and account though the log-likelihood.

I’m not sure how JAGS approaches this (imputes based on values from uncensored data, or integrates out and accounts on log-likelihood). I have attempted to implement imputation outside the default class however the results are no where as close as below.

It’s either that, or differences between Gibbs and No U-Turn Samplers?

Anyway, here is the data so far. The differences are small enough that at the end of the day, I can’t see the end interpretation being different. But I do like consistency.

If anyone has insight, would be amazing.

Data set:

webexpo_compare_data = ['<25.7', '17.1', '168', '85.3', '66.4',  '<49.8',  '33.2', '<24.4', '38.3']

python_vs_r
python_vs_r3634×2434 213 KB

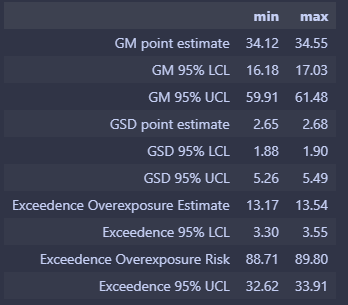
Here are the range of estimates after 50 simulations with the same parameters as the WebExpo report.

  • GM point estimate (33.587 33.958)
  • GM 95% LCL (14.183 14.934)
  • GM 95% UCL (61.723 62.754)
  • GSD point estimate (2.802 2.838)
  • GSD 95% LCL (1.888 1.902)
  • GSD 95% UCL (7.561 8.013)
  • Exceedance point estimate (%) (14.233 14.436)
  • Exceedance 95% LCL (%) (3.501 3.614)
  • Exceedance 95% UCL (%) (35.482 36.178)

Not sure how much my Python is, but here is my model/script.

@dataclass
class CensoredData:
    y: List[float]
    lower_limits: List[float]
    upper_limits: List[float]

def define_observed_lower_upper(expo_data: List[str], oel:float) -> CensoredData:
    y = []
    lower_limits = []
    upper_limits = []

    for value in expo_data:
        if value.startswith('<'):
            # Left-censored
            limit = float(value[1:])  # Extract the numeric value
            y.append(limit)
            lower_limits.append(limit)
            upper_limits.append(np.inf)
        elif value.startswith('>'):
            # Right-censored
            limit = float(value[1:])  # Extract the numeric value
            y.append(limit)
            lower_limits.append(-np.inf)
            upper_limits.append(limit)
        elif '-' in value:
            # Interval-censored
            lower, upper = map(float, value.split('-'))  # Extract the range
            y.append((lower + upper) / 2)
            lower_limits.append(lower)
            upper_limits.append(upper)
        else:
            # Uncensored
            y.append(float(value))
            lower_limits.append(-np.inf)
            upper_limits.append(np.inf)
        
    # Divide all values by the OEL, excluding infinite values
    y = [value / oel if value != np.inf and value != -np.inf else value for value in y]
    lower_limits = [value / oel if value != np.inf and value != -np.inf else value for value in lower_limits]
    upper_limits = [value / oel if value != np.inf and value != -np.inf else value for value in upper_limits]
    
    return CensoredData(y,lower_limits, upper_limits)


data = define_observed_lower_upper(webexpo_between_model_data, 100)

with pm.Model() as model:
    # Priors
    mu = pm.Uniform("mu", lower=-20.0, upper=20.0)
    log_sigma = pm.Normal("log_sigma", mu=-0.1744, sigma= 2.5523)
    sigma = pm.Deterministic("sigma", pm.math.exp(log_sigma))
    precision = pm.Deterministic("precision", 1 / (sigma ** 2))

    # Likelihood with censoring
    censored_observations = pm.Censored(
        "y",
        pm.Lognormal.dist(mu=mu, tau=precision),
        lower= data.lower_limits,
        upper= data.upper_limits,
        observed=data.y,
    )
    
    # Sampling
    
    trace = pm.sample(
        draws=25000, 
        tune=5000, 
        chains=4, 
        return_inferencedata=True,
        initvals={
            "mu": np.log(0.3), 
            "log_sigma": np.log(2.5)
            },
        nuts_sampler='blackjax'
        )
2

Hello Sebastian,

Apologies for the late answer.

First congratulations on the python code !

I am going to have a look at what STAN yields for that sample.

On your side : does the discrepancy disappear if you eliminate the non-detects ?

For JAGs, the current Expostats code indeed imputes non-detects, but in theory it should be numerically equivalent to modifying the likelihood directly.

I agree with your bottom line that this difference shouldn’t matter much, but it’d be better to be able to understand it.

I will return with the STAN results

Cheers,

3

I think I got it :

Its a difference in the normal distributon specification in JAGS vs Python :

in JAGS a normal distribution is defined by mean and precision (not intuitive but historical / bayesian habit I guess), in python it seems it is defined by mean and sd.

I ran the expostats function with precision = 1/sqrt(2.5523), since in your code you define sd=2.5523 and I find results within the range of your simulation.

If I am right your code should look like below to reproduce expostats :

log_sigma = pm.Normal("log_sigma", mu=-0.1744, sigma= 1/sqrt(2.5523))

I went fast so I may have blundered, can you take a look ?

1 Like
4

There we go! Annoyingly enough I later optimised out the tau (precision) deterministic prior step for the likelihood due to this but I missed this completely.

I re-ran my simulation with 50 iterations and got the same coverage as R+JAGS / R.

image

Finished code:

with pm.Model() as no_error_model:
    # Data
    y_data = pm.Data("sampling data", data.y)

    # Priors
    mu = pm.Uniform("mu", lower=-20.0, upper=20.0)
    log_sigma = pm.Normal("log_sigma", mu=-0.1744, sigma= 1/pm.math.sqrt(2.5523))
    sigma = pm.Deterministic("sigma", pm.math.exp(log_sigma))
    # Unlike JAGS, PyMC can use the sigma directly
    #precision = pm.Deterministic("precision (tau)", 1 / (sigma ** 2))
    
    # Likelihood with censoring
    observations = pm.Censored(
        "observations_with_censoring",
        pm.Lognormal.dist(mu=mu, sigma=sigma),
        lower= data.lower_limits,
        upper= data.upper_limits,
        observed=y_data
    )
    
    # Sampling
    
    no_error_trace = pm.sample(
        draws=10000, 
        tune=5000, 
        chains=4,
        initvals={
            "mu": np.log(0.3), 
            "log_sigma": np.log(2.5)
            })
1 Like